ゆたりんブログ

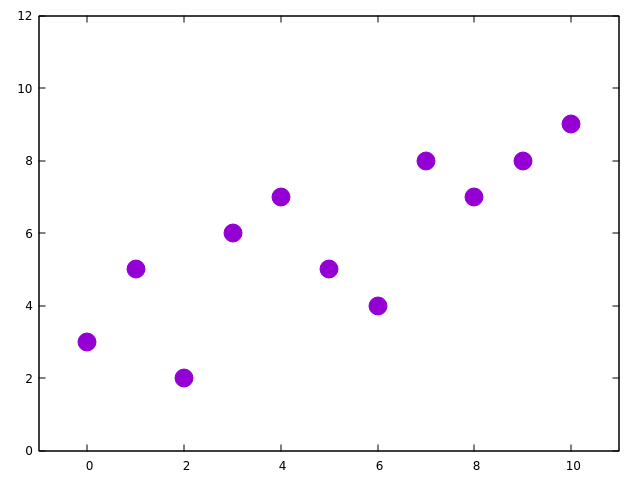
データプロットを関数(ax + b)でフィッティング 始めに  最小二乗法を用いた数値解析によるフィッティングを可視化してみることにしました。 実験で得られた測定データ、表計算や解析ソフトでは簡単に近似曲線と関数が得ることが出来ます。こういうのは実際どういった処理で求めているのかを意識することは無いかも知れません。ただあまりブラックボックスな技術にばかり頼りっきりでもしょうがないので、ちょっと試しに可視化してみることにしました。 用いるデータ さて、用いたデータプロットは以下のようになっています。これを 関数 f(x) = ax + b でフィッティング、つまり最適解となる変数a, bを求めます。 用いるデータプロット ここでは最小二乗法については説明しませんが、手順としてはまず適当にaとbをそれぞれある値に決めます。そこで定まった関数とデータプロットの各点との差を求めます。ここで差は二乗してデータプロット全ての点のそれを合計します(便宜上sumと置く)。そうするとa, b, sumのワンセットが得られます。あとはこれをa, bの値をそれぞれ変化させて、どのパラメーターを取ればsumが最小となるかを求めてそれを解とします。 可視化してみる   解だけ求めるなら計算してsumが最小となる点を抽出すればいいのですが、その過程を可視化するためにもう少し準備をします。  まず計算により得られるデータセットは以下の3列からなります。 a1, b1, sum1 a2, b2, sum2 a3, b3, sum3 a4, b4, sum4 ︙ なので、aをx、bをy、sumをzとして三次元プロットをしてみます。計算過程を動画にすると以下のようになります(左側がデータプロットと関数の二次元プロット、右側が三次元プロット)。左側のグラフではデータプロットの各点と関数との差を矢印で図示するようにしています。 (Youtubeにアップロードした動画、処理にはPythonによるプログラミングも併用)  この動画では大雑把にaとbの範囲を設定して計算しているので、どこが最小なのかはいまいち分かり難くなっています。これは、データプロットから大きく外れたときのsumの値がかなり大きくなるので、全部一つの三次元プロットにしてしま

屋外の温度を測りたいので  6月も後半で梅雨の時期らしく雨に日が多くなってきた感じ。 家庭菜園でちょっとばかり野菜を育てている関係上、外の温度がどれくらいなのか気になるところ。あまり気温が上がらない日が続くと生育が遅れがちになってしまいます。まぁだからといってもこればかりは自然相手なので、対処するのも手段は限られるわけですが。  さて、屋外の気温を調べる場合は気象庁のアメダスのデータで大体は把握出来るのですが、ここの場所は観測点からはちょっと離れているので一応どれくらい差があるものか確認しておきたいです。温度を測るとき、正確性を持たせるなら地上からの高さや日差しを遮るなどいろいろ条件を整える必要があるのですが、簡単に温度計を外に吊るしておくだけにしておきます。  とまぁアメダス観測点との違いを調べるかのように書いてますが、今回のブログで主に調べるのは後述するように温度計が示す温度の安定するまでの時間についてになります。 温度計が安定するまでの時間  さて、温度計を外に吊るしておくだけならすぐに出来るわけですが、外に吊るしたからといっても即座にそこの温度を示すわけではありません。温度計がそこの温度を示すまでにはある程度の時間を要するはず。室温30℃に置いていた温度計を、外気温0℃の外に吊るしてもすぐに0℃になるわけではないですから。このへんは温度計測定部の応答速度や、温度計外装(プラスチック部分など)がそこの温度と熱平衡になるまで待つ必要があったりとか関係してきます。なので、外に吊るした温度計が一体どれくらいの時間でそこの温度を示すようになるのか確認してみることにします。 (おそらく時間は一定ではなく、温度差や風のあるなし、日光などに影響されるでしょう) 用いる温度計と測定方法 温度計 とりあえず、部屋にあったこの温度計を使うことにしました。温度の他に湿度も測れます。この温度計、測定原理はたぶんバイメタル方式だと思います。あとはこれを外に吊るして、経過時間とともにそのときに示している温度を記録していきます。 測定結果  測定といってもそう大したものでもないですが、一応結果としては以下のグラフのようになりました。 温度(℃)、湿度(%)と経過時間の関係  室温が25.5℃あったところから温度計を外に吊るしたわけです

ジョージアと聞いて思い浮かべる場所  ニュースなどで「ジョージア」という地名が出てくることがあります。さて、その地名を聞いたときに、具体的にはどこのことを思い浮かべますか？  この問い、話としては「ジョージア」という地名が複数あることから、人によって思い浮かべる場所が違ったりします。 2つのジョージア  広く知られているジョージアは次の2つ 旧ソビエト連邦から独立したジョージア国(東ヨーロッパ、黒海の東岸に位置) アメリカ合衆国のジョージア州(アメリカ南東部、州都アトランタ)  なお、東ヨーロッパのジョージア国は以前は「グルジア」と呼ばれていました。日本における国名の扱いが切り替わったのが2015年なので、新しい呼び方の方は馴染みが薄いかも知れません。日本語の読みがグルジアでもジョージアでも英語名の綴りは同じ Georgia。そして、グルジアはロシア語読み、ジョージアは英語読みのようです。なぜ呼び方が切り替わったかについては、その国の事情や国際関係などがあるようで、そのへんは歴史的経緯などが絡み複雑なようです。 参考サイト ジョージア ｜ 外務省 ジョージア (国) - Wikipedia ジョージア州 - Wikipedia

グラフウィンドウでのキーボード、マウス操作  gnuplotではQtやX11のようなウィンドウにグラフを出力する出力端末ではグラフ上でキーボード、マウスによる操作が可能です。マウス操作は以下の設定で行えるようになります。これはデフォルトでONになっているので、通常はそのままでマウス操作が行なえます。 gnuplot> set mouse この基本設定にオプションを付けることで操作のカスタマイズが行えるようになっています。今回は基本操作やカスタマイズについていくつか解説していきます。 操作状況を詳しく表示(verboseオプション)  以下のコマンドにより、グラフウィンドウ上でどのような操作をしたのかを実行端末に表示させることが出来ます。 gnuplot> set mouse verbose  デフォルトではこの設定はOFFになっていますが、始めのうちは有効にしておいた方がどんな操作をしているのか分かりやすいです。 (グラフウィンドウ上でキーボードの"6"キーを押しても設定を有効に出来ます) (このスクリーンショットでは"set mouse verbose labels"と"labels"オプションも付けていますが、こうすると後述するラベル追加も表示対象となります) 拡大(ズーム)操作  グラフの特定の範囲を拡大したいときは、拡大したい場所の端で右クリックを押し、カーソルを動かして範囲を決めて再度右クリックを押すとその範囲が拡大されます。  この他に拡大したい場所にマウスカーソルを合わせ、Ctrlキーを押しながらホイールボタンのホイール操作をすることでも拡大と縮小が行なえます。この操作の他に"+"、"="キーで拡大、"-"キーで縮小が行えます。  また、拡大したのを解除して元の表示範囲に戻す場合はグラフ上で"u"キーを押します。 座標のラベルを追加(ミドルクリック)  グラフ上でマウスのミドルボタン(ホイールボタン)をクリックすると、その位置の座標がグラフ上にラベルとして追加されます。  また以下のコマンドを実行しておくと、ラベルの追加の他に削除も行うことが出

gnuplotのグリッド線の描き方  gnuplotはデフォルトではグラフにグリッド線が描かれない設定になっています。ここではグリッド線を有効にする設定を解説していきます。 グリッド線の例 グリッド線の設定方法 簡単には以下のようにsetコマンドでグリッド線を有効に出来ます。 gnuplot> set grid グリッド線の線幅を変えたい場合は "linewidth" オプションの設定を追加します。 gnuplot> set grid linewidth 3 線の色を変えたい場合は "linecolor" オプションを追加。 gnuplot> set grid linecolor "dark-red" 点線ではなく実線にするには以下のようにします。 gnuplot> set grid linetype 1 linecolor 0 主目盛りだけでなく副目盛りにもグリッド線を設定する  ここまで解説した方法ではグリッド線は主目盛りにのみ設定されます。副目盛りにもグリッド線を描く場合、まず副目盛りを設定します。 副目盛りの設定 副目盛りを設定するにはx軸には gnuplot> set mxtics y軸には gnuplot> set mytics とします。 (副目盛りの数、間隔も別途設定出来ますが、今回はグリッド線の説明のためそれらの解説は省きます) 設定した副目盛りに対してグリッド線を設定 副目盛りの設定をしたなら次は副目盛りのグリッド線設定を行っていきます。 x軸、y軸に主目盛りに加えて副目盛りにもグリッド線を描くコマンドは以下のようになります。 gnuplot> set grid xtics mxtics gnuplot> set grid ytics mytics 副目盛りに個別に線の設定をするには、以下のようにカンマで区切って主目盛りと副目盛りのそれぞれの線の設定を行ないます。 gnuplot> set grid xtics mxtics linewidth 2, linewidth 1 グリッド線設定の確認方法 グリッド線がどのような設定になっているのか

 このブログ記事は個人的な勉強のメモ書き、覚え書き程度のものです。内容の正確性などあまり当てにならない面が多いので、ちゃんとしている情報を知りたい場合は他のサイトを探して下さい。 Javascriptで特定の要素の表示、非表示を切り替える処理  HTMLのコードに、以下のようなHTML要素(div)をあるときは表示、またあるときは非表示にすることを考える。 <div id="test01"> <h2>タイトル1 </h2> 本文1 </div>  また、ここで表示切り替えに以下のチェックボックスを用意する。 <input type="checkbox" onclick="func_show01()" checked>テスト<br> チェックボックスが押されたときに"func_show01()"関数が実行される。今回考える処理ではチェックボックスがONかOFFかは考慮せず、関数が実行されたときに表示、非表示が切り替わるようにする。 (今回はそうするというだけで、ON、OFF状態を取得して切り替えても良い)  そして、Javascript側の関数での処理は以下のようになる。  function func_show01() {   var s = document.getElementById("test01");   if (s.style.display === "none") {     s.style.display = "block";   } else {     s.style.display = "none";   } } 処理の流れとしては チェックボックスのON、OFFで関数"func_show01()"が実行 ↓ 関数内でまず要素divのidが"test01"のElementオブジェクトを変数sに取得 ↓ style.displayメソッドで変数sの表示、非表示状態を判定 ↓ ifにより表示の場合は非表示に、非表示の

甘酢炒めを作ろうと思った次第 ジメジメした日が続いて少し食欲が落ち気味なので、酸っぱいものでも作ろうかと思い野菜の甘酢炒めを作ることに。買っておいたニンジンとピーマンもそろそろ食べてしまわないと悪くなりそうだったというのも甘酢炒めを作ろうと思った理由。 甘酢炒めの材料 今回の食材としては タマネギ　1個 ニンジン　1本 ピーマン　3個 キャベツの芯　ちょこっと 調味料は 水　100ml ケチャップ　大さじ4 酢　大さじ4 砂糖　大さじ3 醤油　小さじ1 みりん　大さじ1 固形コンソメ　1個 それと最後にまとめる用に 片栗粉　大さじ1 料理手順  まず調味料を合わせて合わせ調味料を作る。ただ固形コンソメをそのまま入れても全然溶けなかったので、全部合わせた後で火にかけてコンソメを溶かした。参考にしたレシピでは酒を入れることになってたけどあいにくと酒は無かったのでみりんで代用。その分、砂糖を気持ち減らした。  野菜はまずニンジンを下茹で(5分くらい)。あとキャベツの千切りで余った芯も下茹でして入れることに。で、タマネギ、ピーマンも適当な大きさに切って、フライパンに油をしいて炒める。  夕飯にはまだ早いのでここで一旦作業中断。  1時間ほど後、フライパンの中のタマネギがかなり透明でクタクタしてしまっていた…。違う、イメージしていた甘酢炒めのタマネギはもっとこう原型を保っているので、これは何か違う…。まぁなってしまったことはしょうがないので、これはこれでいいだろうということにして作業続行。  フライパンを火にかけそれとなく温まったところに合わせ調味料を入れて、味が馴染むまで数分煮ていく。最後に水で溶かした片栗粉でまとめて完成。 仕上がりの感想  さて、作ってみた野菜の甘酢炒めを感想だけど、やはりタマネギの存在感が無い…。炒めた時点であそこまでクタクタになっていて、さらに合わせ調味料と煮ていたのだからしょうがないと言えばしょうがない。ここは次回への反省点。目標としては、タマネギの原型を保ちつつ、かといって生の辛味を感じさせないように火を通し、クタクタになる直前のシャッキリ感で仕上げる。うーん、なかなか難しそう。  それと、味に関しては結構いい感じ。ただ食べ進めていくと酸っぱさよりも甘さの

 このブログ記事は個人的な勉強のメモ書き、覚え書き程度のものです。内容の正確性などあまり当てにならない面が多いので、ちゃんとしている情報を知りたい場合は他のサイトを探して下さい。 段落や行中の文を指定する要素  HTMLである段落(任意の領域の文章)や行の中の文を要素として扱いたいとき、 div (段落) span (行中) を用いる。CSSで要素の装飾などしたいとき、これにidなど付けておけば特定の場所の文章を指定しやすくなる。

 このブログ記事は個人的な勉強のメモ書き、覚え書き程度のものです。内容の正確性などあまり当てにならない面が多いので、ちゃんとしている情報を知りたい場合は他のサイトを探して下さい。 Textarea要素とは  Textarea要素とは以下のようなテキストインプットフォームのこと。 これがTextarea要素  このTextareaは掲示板サイトやアンケート、各種項目入力のコメント入力に用いられている。通常は送信ボタンが付いていて、それを押すことでサイト側に入力したテキストが渡される。 CSSでTextarea要素を設定するには  簡単には以下のように指定する。 textarea {    font-size: 20px; }

Dockランチャーでアプリアイコンが複数出来てしまう状況  GNOMEデスクトップ環境のDockランチャーで、まれにアプリアイコンが複数出来てしまうことがある。複数出来てしまう状況としては、アプリをお気に入り(favorite)として登録(ピン止め)してそこからアプリを起動するとお気に入りの他に別にアプリアイコンが出来てしまうことなど。  原因としては、起動したアプリウィンドウのグループ化がうまくいっていないことによるらしい。調べても理解が難しそうだったので解説は割愛。  この現象が起きるのは特定のアプリに限られるようなので、通常はまったく問題が起きないことの方が多いと思われる。自分でカスタムアプリアイコンを作ったりする場合には起こりやすいのかなと思う。 対策(***.desktopファイルを編集する)  アプリ起動に用いる ***.desktopファイル(***は任意の名前。firefoxならfirefox.desktop)に以下の項目を作成することで避けられる模様。 StartupWMClass この項目を設定するにはアプリ毎の設定値が必要で、その設定値は以下のコマンドで得ることが出来る。ここで調べたいアプリを起動してウィンドを前面に出しておく。 $ xprop WM_CLASS このコマンドを実行するとマウスカーソルが変化するので、調べたいアプリウィンドウ上でクリックすると WM_CLASS(STRING) というカタチで設定値が得られる。この設定値を先程の ***.desktopファイルの StartupWMClassに設定する。 (設定値が複数取得される場合、どちらか一方でもいいかも。詳しくは不明)

朝から雨降りで、どうやら今年も梅雨の季節となってきたようです。 5月後半は30℃超えのやたら暑い日が続いたけど、6月はどうなるでしょうか。 梅雨寒となるか蒸し暑くなるか、雨は多いのか少ないのかなどなど気になるところ。 このへんは気象庁が長期予報を出してるので、そういうのを参考にするのがいいのかなと。 まぁ予報はあくまでも予報なわけですが。  そしてまだ雨が降っていた昼過ぎごろ、外を歩いていたらコンクリート壁にカタツムリが数匹くっついてるのを見かけました。 晴れてるときは全然姿が見えなかったけど、雨だとやっぱり出てきますね。普段は石の下とかにでもいるんでしょうか。 梅雨の時期は食べ物を出しっぱなしにしているとすぐ悪くなってしまうし、ジメジメして気が滅入ることもあったり。それでも雨の降る音を聞いたり、川の流れを眺めたりなど季節を感じるのもまた一興。 個人的には家庭菜園で育ててる野菜や花に水をやる手間が減るので、その点では雨降りは助かると言えば助かります。あまり雨降りが続き過ぎるのはそれはそれで困りますが。あと伸びるのは野菜ばかりじゃなく、雑草の伸びも大きくなるのでそれも一つの悩みの種。蒸し暑い中での草刈りは結構大変なわけで。

gnuplotでコマンドやオプションを省略した書き方  gnuplotではコマンドやオプションを省略して短く書くことが出来ます。例えば "plot" の場合は "p", "with" の場合は "w" などです。どこまで短く書けるかですが、他のコマンドやオプション名と被らないところまで短く出来るようです。また可能な限り短くする必要はなく、"plot" を例にすると p pl plo が同様に "plot" として実行されます。  省略した書き方はそれをそれとして分かっていれば、コマンドを書きやすくなります。また、コマンド文を短く出来るので何が省略されているのか分かってさえいれば読みやすくもなります。ただ、しばらくgnuplotを使わずに何の略か忘れてしまうことや、他の人にスクリプトファイルを渡して読んでもらう場合などを考えると、略さずにきっちり書いておいた方がいい場合もあります。個人的には後にスクリプトファイルとして残しておくようなコマンドは略さずにそのまま書いておくようにしています。 省略例  以下にいくつかの省略例を示しておきます。 コマンド plot → p splot → sp set → se title → tit xrange → xr yrange → yr clear → cl break → break cd → cd exit → ex help → h history → hi load → l pause → pa print → pr quit → q show → sh plot関連 with → w using → u プロットスタイル lines → l points → p linespoints → lp vectors → vec impulses → i steps → st boxes → boxes circles

ベクトルプロットでのベクトルの始点の位置 gnuplotのベクトルプロットでのベクトルの始点の位置、データのx, y座標の位置に来ます。 例えばx, y座標が(1, 1)の以下のようなデータの場合、次のグラフのように(1, 1)がベクトルの始点になります。 1 1 1 0 始点がこの位置でいい場合はこれでいいわけですが、場合によっては指定したx, y座標にベクトルの中央が来て欲しい場合もあるでしょう。今回はその方法について解説していきます。  話としては以前の次の記事を下敷きにしています。   gnuplot : ベクトルプロットでのデータの扱い方について(vectors)  今回の話を読んでいて分かり難い場合、まずはこの記事を読んでみて下さい。 x, y座標にベクトルの中央を合わせる  x, y座標にベクトルの中央を合わせるには、ベクトルの始点、つまりx, y座標をずらす操作を行ないます。データ3列目のxdelta、4列目のydeltaはx, y座標とは関係なく、大きさの成分なのでこちらはこのまま用います。ベクトルの中央はxdeltaの1/2、ydeltaの1/2で表されるので、その分をx, y座標から差っ引いて始点をずらします。そうするとusingでは次のように指定すればいいわけです。 using ($1-$3/2.0):($2-$4/2.0):3:4 これでプロットすると以下のグラフとなります。 ベクトルの中央がx, y座標(1, 1)になっているのがわかります。 比較のため、始めのグラフと一緒にプロットすれば以下のようになります。 データがベクトルの大きさと角度の場合  データがxdelta, ydeltaではなくベクトルの大きさと角度の場合でも、変換してベクトルの始点の位置を算出してやれば同様に処理出来ます。 このへんは以前のベクトルの話と被るので詳しくは説明しませんが、usingの指定は次のようになります。 using ($1-($3*cos($4))/2.0):($2-($3*sin($4))/2.0):($3*cos($4)):($3*sin($4)) (角度がラジアンではなく度の場合は設定の変更が必要) (以前の記事 : gnuplot : ベクトルプロットでのデータの扱い方について(vectors) )

ベクトルプロット(Vector plot)とは  gnuplotではvectorsというプロット形式でベクトルプロットを行うことが出来ます。要はある点におけるベクトルの大きさと方向を図示するというもの。 今回はベクトルプロットのプロット時のデータの指定方法について解説していきます。 (ベクトルプロットは3次元プロットでも使えますが、今回は2次元プロットの解説のみになります) ベクトルプロットの例  ベクトルプロットは以下のようなプロットになります。 プロットソースコード $data01 << EOD 0 0 0.4 0.4 0 1 0.1 -0.1 0 2 0.4 0.2 1 0 -0.3 -0.2 1 1 0.2 0.2 1 2 0.3 0.3 2 0 -0.4 0.1 2 1 -0.3 0.4 2 2 0.2 -0.3 3 0 0.3 0.2 3 1 0.4 -0.3 3 2 -0.4 -0.3 EOD unset key set grid set xrange [-0.5:3.5] set yrange [-0.5:2.5] plot $data01 with vectors lc 'red',\ '' with points lt 6 lc 'black' (EODというのはdatablocksというプロットファイルの書き方によるものです。詳しくは次の記事を参照して下さい : gnuplotで一つのファイルにデータとプロットコマンドを含める方法(datablocks) ) プロットデータの説明  ベクトルプロットでは、x, y座標の他にベクトルの大きさと向きを指定する必要があります。gnuplotのベクトルプロットでは、用いるデータは以下の4つの要素が必要になります。 x座標 y座標 xdelta : ベクトルのx方向の大きさ ydelta : ベクトルのy方向の大きさ このうちのxdeltaとydeltaによりベクトルの大きさと方向が決まることになります。 簡単に図で説明すると、次のような関係になっています。 usingを用いた指定 プロット時にはusingを用いて以下のように指定します。 gnuplot> p

とある日の東京の風速と風向き 東京のとある日(2019年6月1日)の風向きと風速からグラフを作ってみました。 データそのままではなく、風をベクトルとして扱い、風向きと風速を元に角度90°ごとに東西南北に要素を分けてグラフ化。こうすることで、どの時間帯でどちら寄りの風が強かったのかが分かるかなと思い作ってみました。 グラフを見ると午前中は北の成分が多く、午後からは南、東の成分が多いことが分かりました。 (実際、風に対してこのような分析が適してるのかまでは調べていないので、あくまでも個人的に参考にする程度のものですが) 用いたデータ 地点 : 東京都 東京 日時 : 2019年6月1日 データ : 風向・風速 (気象庁の「過去の気象データ・ダウンロード」からダウンロード) 気象庁 Japan Meteorological Agency 解析の仕方  データに関しては風向きが東西南北の16方位で格納されているので、まずそれを0〜360°の角度に変換(Pythonで変換用プログラムを作成)。角度を元に風速をかけ合わせ、それをsin,cos関数でx, y成分に分離。+yが北、-yが南、+xが東、-xが西となるよう振り分けて一時データファイルとして保存。それをgnuplotでグラフ化という手順で行ないました。 プロット形式はfilledcurveとvectorsを用いました。 gnuplot関連のブログ記事